|
The decimal mathematical system widely used today originated by counting with the fingers a person has. Counting with the fingers and toes started the Maya vigesimal system. So it is based on groups of twenty units. Just as the decimal system goes by 1, 10, 100, 1000, 10000, etc., the Maya vigesimal system goes 1, 20, 400, 8000, 160000, etc. While in the decimal system there are ten possible digits for each placeholder [0 - 9], in the Maya vigesimal system each placeholder has a possible twenty digits [0 - 19]. For example, in the decimal system 31 = 10 * 3 + 1 while in the vigesimal system 31 = 20 + 11. The Maya discovered and used the zero. Their zero is represented by an ovular shell. Characteristics of The Maya Mathematical System: a) It is vigesimal, this means that it is based on 20 units [0 - 19] instead of the 10 units [0 - 9] of the decimal system. This table shows the first 20 numbers and their Arabic equivalents. Learn the Maya mathematical system fast using THE MAYA CALCULATION ASSISTANT. The Mayan names for numbers are here.
b) It only uses three symbols, alone or combined, to write any number.
These are: the dot - worth 1 unit, the bar - worth 5 units and the zero
simbolized by a shell.
d) Numbers in the Maya system can be written vertically or horizontally. In vertical writing, the bars are placed horizontally and the dots go on top of them, in this case the vigesimal positions grow up from the base. When written horizontally, the bars are placed vertically and the dots go to their left and higher vigesimal positions grow to the left of the first entry.
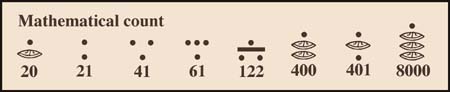
Thus when writing vertically the vigesimal positioning system, to write 20 a zero is placed in the first position (base) with a dot on top of it, in the second position. The dot in this place means one unit of the second order which equals to 20. To write 21, the zero would change to a dot (1 unit) and for the subsequent numbers the original 19 number count will follow in the first position. As they in turn reach 19 again another unit (dot) is added to the second position. Any number higher than 19 units in the second position is written using units of the third position. A unit of the third position is worth 400 (20 x 20), so to write 401 a dot goes in the first position, a zero in the second and a dot in the third. Positions higher than the third also grow multiplied by twenties from the previous ones. Examples of the numbers mentioned above follow:
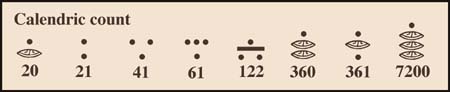
(Note : the Maya made one exception to this order, only in their calendric calculations they gave the third position a value of 360 instead of 400, the higher positions though, are also multiplied by 20.)
|